OPEN CIRCUIT CHARACTERISTICS OF POWER TRANSFORMER BASIC INFORMATION

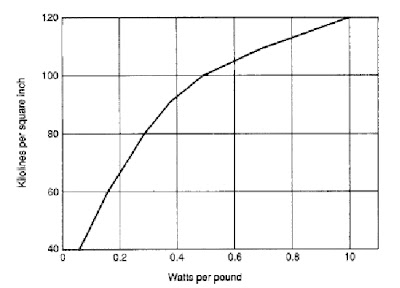
The core loss (no-load loss) of a power transformer may be obtained from an empirical design curve of watts per pound of core steel (Fig. below). Such curves are established by plotting data obtained from transformers of similar construction.

  

The basic loss level is determined by the grade of core steel used and is further influenced by the number and type of joints employed in construction of the core. Figure 10-1 applies for 9-mil-thick M 3-grade steel in a single-phase core with 45” mitered joints.

Loss for the same grade of steel in a 3-phase core would usually be 5% to 10% higher. Exciting current for a power transformer may be established from a similar empirical curve of exciting volt-amperes per pound of core steel.

The steel grade and core construction are the same as for Fig. 10-1. The exciting current characteristic is influenced primarily by the number, type, and quality of the core joints, and only secondarily by the grade of steel.

Because of the more complex joints in the 3-phase core, the exciting volt-amperes will be approximately 50% higher than for the single-phase core. The exciting current of a transformer contains many harmonic components because of the greatly varying permeability of the steel.

For most purposes, it is satisfactory to neglect the harmonics and assume a sinusoidal exciting current of the same effective value. This current may be regarded as composed of a core-loss component in phase with the induced voltage (90DEG ahead of the flux) and a magnetizing component in phase with the flux.

Sometimes it is necessary to consider the harmonics of exciting current to avoid inductive interference with communication circuits. The harmonic content of the exciting current increases as the peak flux density is increased.

Performance can be predicted by comparison with test data from previous designs using similar core steel and similar construction. The largest harmonic component of the exciting current is the third.

Higher-order harmonics are progressively smaller. For balanced 3-phase transformer banks, the third harmonic components

EFFECTS OF HARMONICS ON TRANSFORMERS BASIC INFORMATION AND TUTORIALS

The effects of harmonics on transformers are

• Increased copper losses

• Increased iron losses

• Possibly resonance between transformers

• windings and line capacitance

• Insulation stress

• Neutral overheating due to triplen harmonics

The copper losses and iron losses in the presence of harmonics can be computed. The application

of general equations assumes that the transformer is a linear device which it is not. However, for normal, operating conditions and normal levels of harmonics, this is a reasonable approximation.

However, the increase of hysteresis losses due to harmonics is only a fraction of the eddy current losses. Voltage harmonics result in higher transformer voltage, therefore higher insulation stress. This is not a problem since most transformers are insulated for much higher voltage levels than the overvoltages due to usual levels of harmonics.

There is a certain degree of interaction between voltage and current harmonics for transformers designed to operate near the saturation point (knee of the saturation curve). It is possible a small level of voltage harmonic to generate a high level of current harmonics. This phenomenon depends on specific harmonic and phase relationship to the fundamental.

To address the overheating of transformers due to harmonics, the ANSI/IEEE published a standard C57.110-1998, “Recommended practice for establishing transformer capability when supplying nonsinusoidal load currents,” which was reaffirmed in 2004. This standard establishes methods for determining derating factors for transformer capability to carry nonsinusoidal load currents.

In 1990, Underwriters Laboratory (UL) established the method for testing transformers that serve nonlinear loads. The UL test addresses coil heating due to nonlinear loads and overheating of the neutral conductor by assigning a “K“ factor to the transformer. The K-factor is meant to apply to transformers serving general nonlinear loads. UL has devised the K-factor method for labeling and rating the ability of dry-type transformers to withstand the effects of harmonics.

The K-factor rating indicates the transformer’s ability to tolerate the additional heating caused by harmonics. The K-factor is based on the methodology similar to that discussed in the ANSI/IEEE C57.110 standard. The K-factor can be calculated as the sum of the product of each harmonic current squared and that harmonic number squared for all harmonics from the fundamental to the highest harmonic of consequence.

When K-factor is multiplied by the stray losses of the transformer, the result represents the total stray losses in the transformer caused by harmonic currents. To obtain the total load losses, the total stray losses are then added to the load losses. It should be obvious that the K-factor for linear loads (absence of harmonics) is 1.

Also, the K-factor does not mean that the transformer can eliminate harmonics. Harmonics increase heating losses in all transformers, and some of these losses are deep within the core and windings and some are closer to the surface. Oil-filled transformers react differently to the increased heat and are better able to cool whereas dry-type transformers are more susceptible to the harmonic current effects and are so labeled. The UL test addresses coil heating due to nonlinear loads and overheating of the neutral conductor.